The lambda (λ) is an iconic symbol of the Half-Life series, forming part of the logo for all of the games to date, being displayed on the chest of the HEV suit, and signifying the resistance movement in Half-Life 2 and it’s episodes, not to mention being the main logo of a certain Valve fansite.
But what does this logo mean, exactly, outside of Half-Life?
The Lambda symbol, ‘λ’ is the eleventh letter in the Greek alphabet, from which the letter L of the latin alphabet stems, and has many different uses in various subjects in science and mathematics. In this article, I hope to discuss just a couple of those uses. For science of course!
One use of lambda that anybody who has studied physics should be familiar with is wavelength. A wave is an oscillation that travels through space, and transfers energy. Examples of waves include water waves, such as those which form on the surface of a pond, sound waves, electromagnetic waves, such as light, and more.
Wavelength is defined as the distance from the crest to crest or trough to trough of a sinusoidal wave, commonly with units of meters (m).
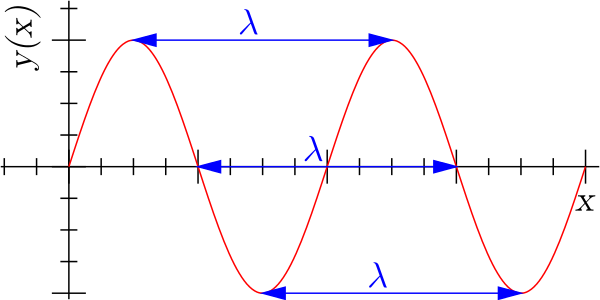
In the case of sound waves, the wavelength affects the pitch of the sound. A longer wavelength means that waves are less frequent (frequency is inversely proportional to wavelength), and thus sound has a lower pitch. A shorter wavelength, however, means a higher frequency, and thus the pitch of the sound is higher.
The wavelength also determines the colour of light which we perceive. At one end of the visible part of the electromagnetic spectrum is the colour violet, which occurs at shorter wavelengths of about 400 nanometers. At the other end is red, at around 650 nanometers.
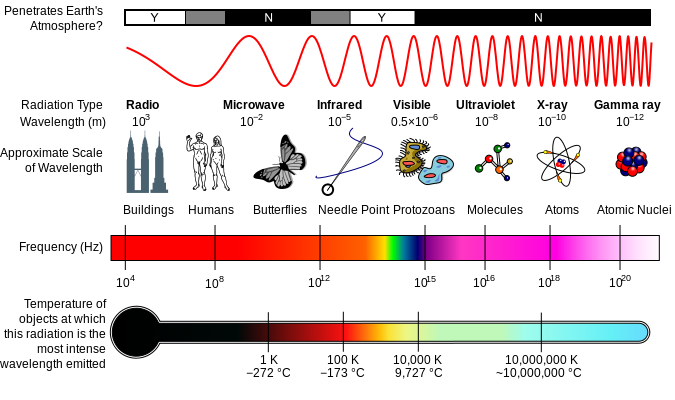
The portion of the electromagnetic spectrum that we can see, however, is just a small part of the spectrum. At wavelengths shorter than 400 nanometers, there is ultraviolet radiation, X-rays and gamma rays. At wavelengths longer than 700 nanometers, there is infrared radiation, microwaves, and radio waves. All of these different forms of radiation are electromagnetic waves with different wavelengths and frequencies.
The lambda symbol also represents the exponential decay constant, in situations when a quantity decreases exponentially, or as Wikipedia states, “at a rate proportional to its current value.”
Radioactive materials undergo decay. Such elements have unstable atoms, and the nuclei of the unstable atoms break down, losing mass and energy in the form of radiation. On larger scales, the decay of radioactive substances can be modelled as exponential decay. The exponential decay constant is the rate at which the quantity decays. At larger exponential decay constants, the quantity decays more rapidly.
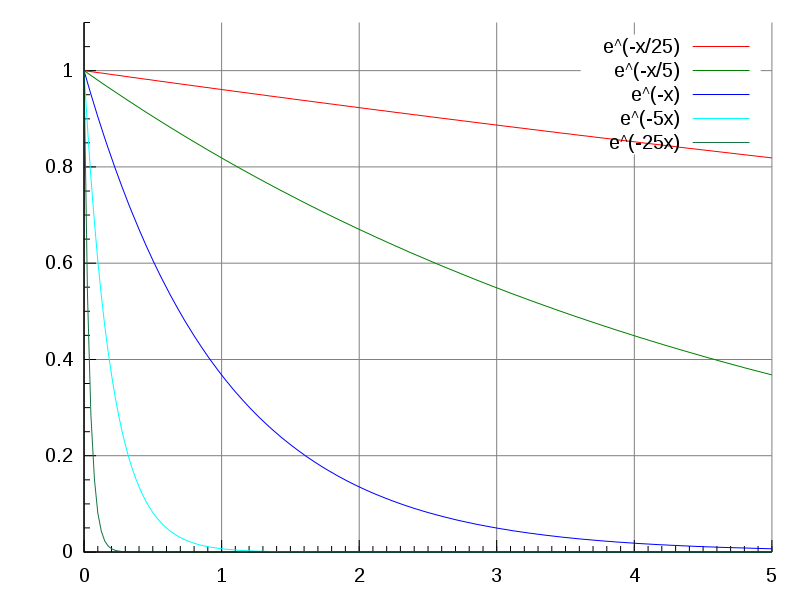
A quantity’s half-life (sound familiar?) is related to the decay constant. It is the time it takes for the quantity, undergoing exponential decay, to decrease to half of its current amount. The term is commonly used when discussing radioactive elements, as different elements have different half-lives.
The last topic I will mention is in the field of biology: the lambda phage. A bacteriophage is virus which infects bacteria cells. They infect cells by attaching to them and injecting their genome, consisting of DNA or RNA into the cell’s cytoplasm, the gel-like substance enclosed inside the cell.
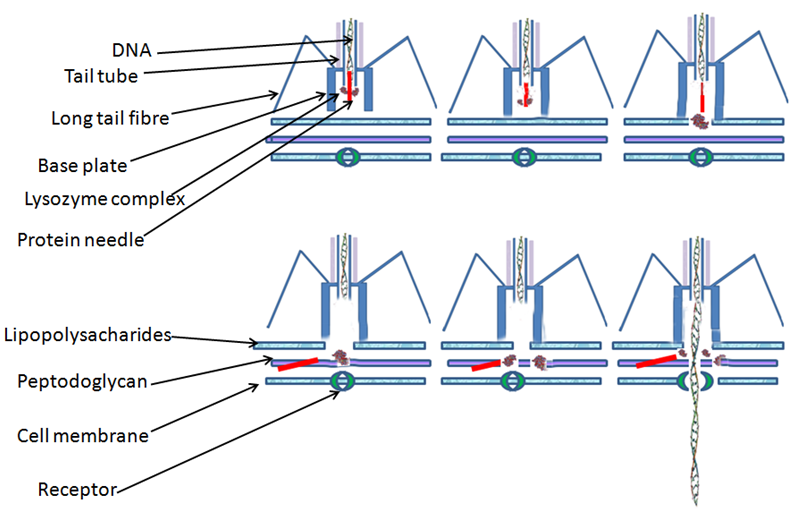
Once inside the cell, the genetic material is translated into proteins, and new bacteriophages are produced. Finally, the new phages exit the cell, usually by breaking down the cell membrane and exiting, called lysis, and then go on to infect other cells. The lambda phage is one such bacteriophage, which specifically targets E. Coli cells.
Cells are able to resist infection from bacteriophages with restriction enzymes, enzymes that slice any foreign DNA into small pieces, thus preventing them from producing more bacteriophages. In order to prevent restriction enzymes from slicing up the DNA of the cell itself, the cell’s DNA contains certain protective organic compounds, methyls, preventing the restriction enzymes from binding.
Well, that’s all for now. I hope that you found my examples interesting, and weren’t bored to tears by my dry technical descriptions. Science is interesting, and Half-Life, while not an incredibly scientifically realistic work, certainly has a lot of scientific references that are worth discussing.
Please feel free to join in, and share any other uses of the symbol lambda that you find particularly interesting in the comments below.
FOR SCIENCE!
I have 3 other examples that crossed my mind when I read this:
– Lambda calculus ( https://en.wikipedia.org/wiki/Lambda_calculus ) is a typical way to deal with functions particularly in some functional programming languages (haskell; go look their icon because… well lambda stuffs)
– In statistics, a Poisson distribution (named after his creator) has lambda as a parameter ( https://en.wikipedia.org/wiki/Poisson_distribution )
– Lastly in linear algebra, one would call lambda the eigenvalue of A in the equation Ax = λx (A is a matrix of size n x n and x is a non-zero vector) ( https://en.wikipedia.org/wiki/Eigenvalue )
Very interesting. It actually occurred to me to mention eigenvalues and eigenvectors, but it was difficult to explain concisely. 😛
I have to admit it required me to dig into my books to remind me about this topic.
An excellent article! As an aspiring physicist myself it is good to see some science on the site – GLaDOS would be proud!
Why thank you, and good luck with physics!
Gay pride!
Ah yes, it’s an LGBT symbol as well. Thank you!